DeBERTa 论文解读

《Deberta: decoding-Enhanced Bert with Disentangled Attention》，该论文来自 ICLR2021，作者团队为微软，主要介绍了其提出的一个新的预训练语言模型：DeBERTa，该模型从注意力解耦（disentangled attention）和预训练阶段的解码增强两方面对BERT类预训练模型进行了优化，并在SuperGLUE上首次超越人类基准。

论文地址、代码地址

一、Introduction

这篇文章的创新点主要在三个部分：1.使用了解耦的注意力机制；2.对预训练阶段的MLM任务的Decoder层进行了改进；3.训练技巧（虚拟对抗训练）

1. 解耦的注意力机制

我们回想 Transformer 的结构，对于一个 token 的表示，是在其 word embedding 的基础上加上 position embedding 所构成的。当然 Vaswani 的 Transformer 对于位置嵌入使用的是绝对位置编码，这种方法饱受质疑，后续又出现了相对位置编码等等。而BERT也是如此，其 word embedding 为 token embedding, position embedding 和 segment embedding 三者的相加。

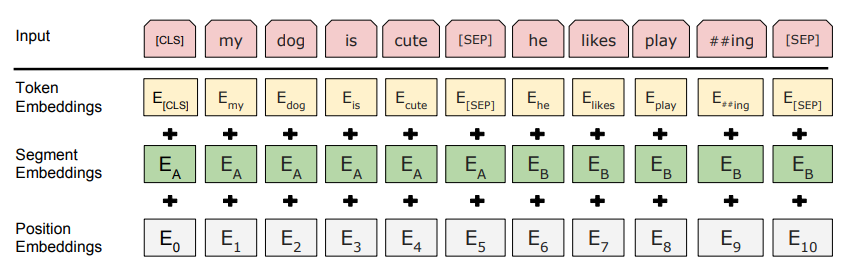
而本文提出的解耦的注意力机制（disentangled attention mechanism）对于位置嵌入的处理方式与上述不同，即不再是在编码阶段简单的将内容嵌入与位置嵌入进行简单的相加作为一个字或词的表示，而是将一个 token 的表示分为两个向量，一个为 content embedding，另一个为 position embedding，二者分别进行注意力计算，之后再进行相加，因此称作解耦的注意力机制。

2. Enhanced Mask Decoder

像 BERT 一样，DeBERTa 在预训练阶段也使用了 Masked Language Modeling（MLM），MLM 其实是一个完形填空任务，需要让模型对于被 mask 掉的位置预测出其原本的单词。但原本的 BERT 中的预测部分，也就是解码部分只有一个简单的 softmax 层，但我们在进行后续下游任务的微调时候，一般都会加一个用于特定任务的解码器，因此本文提出了一个 Enhanced Mask Decoder（EMD）用于预训练阶段，为的就是缓解预训练任务与微调之间的不匹配。

3. SiFT

感觉这算是一个微调的训练技巧吧，作者针对虚拟对抗训练（virtual adversarial training）进行了小部分的调整，新方法称为 Scale-invariant-Fine-Tuning（SiFT）。在针对将预训练模型用于下游任务的Fine-tune阶段加入 SiFT 可以增强模型的泛化性。

二、Background

说实话背景这一块内容并不多，也没有什么值得介绍的，一共就两个，第一个就是目前各大预训练语言模型所使用的 Transformer 模型结构，另一个就是 MLM。关于 Transformer，可以看我的上一篇文章，下面简单用语言和数学公式描述下 MLM：

对于给定一个序列 $ \textit{X} = \lbrace x_i \rbrace $，我们通过随机 mask 掉其 15% 的 tokens，将 $\textit{X}$ 变为 $\tilde{X}$，训练一个模型，模型参数集合为 $\theta$，我们让模型基于 $\tilde{X}$ 来预测被 mask 掉的 $\tilde{x}$，数学描述为：$$ \mathop{max}\limits_{\theta}logp_{\theta}(\textit{X} | \tilde{X}) = \mathop{max}\limits_{\theta}\sum\limits_{i\in\mathcal{C}}logp_{\theta}(\tilde{x_i} = x_i | \tilde{X}) \tag{1}$$ $\mathcal{C}$代表序列中被 mask 掉的 token 的索引，当然这里就不具体展开具体 mask 的规则了。

三、Model Architecture

在这一部分，我们详细介绍一下这篇论文所提出的 DeBERTa 的模型结构，主要分为 Disentangled Attention 和 Enhanced Mask Decoder(EMD) 两个部分。

1. Disentangled Attention

如前所述，所谓解耦的注意力机制，即是将词嵌入解耦为内容嵌入和位置嵌入两个向量，文中小标题这么来概括它："A Two-Vector Approach to Content and Position Embedding"。那么具体是怎么做的呢？

对于一个序列中位置为 $i$ 的 token $x_i$，我们用 $\lbrace \textit{H}_i \rbrace$ 和 $\lbrace \textit{P}_{i|j} \rbrace $ 两个向量来表示它，前者代表它的内容（content）嵌入，后者代表它关于序列中位置为 $j$ 的 token $x_j$ 的相对位置（relative position）嵌入。在之前我们都是将两个向量相加得到的一个和向量作为 token 的编码表示，但现在我们换一个玩法，我们将 content 和 position 看作独立的个体，让他们都参与到 attention 的计算过程中，那么也就得到了下面的公式：$$ \textit{A}_{i, j} = \lbrace \textit{H}_i, \textit{P}_{i|j} \rbrace \times {\lbrace \textit{H}_j, \textit{P}_{j|i} \rbrace}^{T} \\ = \textit{H}_i\textit{H}_j^{T} + \textit{H}_i\textit{P}_{j|i}^{T} + \textit{P}_{i|j}\textit{H}_j^{T} + \textit{P}_{i|j}\textit{P}_{j|i}^{T} \tag{2}$$

如公式（2）所示，使用注意力解耦的方法可以将一个 word pair 的 attention 权重看作四个分量的和：content-to-content, content-to-position, position-to-content 和 position-to-position。在这里作者指出，现有的相对位置嵌入的方法^[1]只在 Attention 计算时用了分离的 Embedding 矩阵，这种做法相当于只用到了前面提到的四个分量中的前两个。但作者认为一个 word pair 之间的 attention 权重不仅依赖于其 content，它们之间的相对位置关系也至关重要，因此加入了第三个分量，也就是 position-to-content。最后丢弃了第四个分量（因为已经是相对位置关系了，位置和位置之间的关系已经提供不了额外的信息了，所以丢弃了这个分量）。

在这里我觉得有必要简单介绍一下Shaw等人^[1]提出的在 Transformer 中使用相对位置嵌入的方法。我们将输入的序列 $ \textit{X} $ 看作一个有向全连接图，对于 $ \textit{X} $ 中的元素 $x_i$ 和 $x_j$ 之间的边通过两个向量 $a_{ij}^K, a_{ij}^V \in \mathbb{R}^{d_a}$ 来表示，并且这些向量在多个 head 之间共享，$d_a = d_z$。通过引入边的特征表示，将 Vaswani 类 Transformer 中的 self-attention 计算方式修改为： $$ z_i = \sum_{j=1}^n\alpha_{ij}(x_jW^V + a_{ij}^V) $$ $$ \alpha_{ij} = \frac{\text{exp}\ e_{ij}}{\sum_{k=1}^n\text{exp}\ e_{i,k}} $$ $$ e_{ij} = \frac{x_iW^Q(x_jW^K + a_{ij}^K)^T}{\sqrt{d_k}} $$

而 $ a_{ij}^K $ 和 $ a_{ij}^V $ 通过以下公式得出： $$ a_{ij}^K = W_{clip(j-i, k)^K} $$ $$ a_{ij}^V = W_{clip(j-i, k)^V} $$ $$ clip(x, k) = max(-k, min(x, k)) \tag{3}$$ 文中提及的已经存在的相对位置嵌入的方法就介绍到这里，下面继续介绍本篇文章提出的 Disentangled Attention。

上接公式（2），我们取其前三个分量作为注意力权重，首先回顾一下标准的单头（single head）自注意力（self-attention）运算^[2]。 $$ Q = HW_q,\ K = HW_k,\ V = HW_v,\ A = \frac{QK^T}{\sqrt{d}} $$ $$ H_o = softmax(A)V $$ $ H \in \mathbb{R}^{N \times d} $ 表示输入的隐层向量，$ H_o \in \mathbb{R}^{N \times d} $ 表示 self-attention 的输出，$ W_q,\ W_k,\ W_v \in \mathbb{R}^{d \times d} $，N代表输入序列的长度。

前面提到，在本篇论文中一个 token 的表示分别用 content 和 position 两个向量表示，因此使用了两套 Q和K，下面用 $Q_c,\ K_c,\ V_c$ 表示关于 content 的矩阵，$Q_r,\ K_r$ 表示关于 position 的矩阵。同时，$W_{q, c},\ W_{k, c},\ W_{v, c} \in \mathbb{R}^{d \times d} $ 用来表示关于 content 的 projection matrices，$W_{q, r},\ W_{k, r} \in \mathbb{R}^{d \times d}$ 用来表示关于 position 的 projection matrices。额外的，定义了一个用于存储位置嵌入的矩阵 $ P \in \mathbb{R}^{2k \times d} $。那么可以得到如下几个公式： $$ Q_c = HW_{q,c},\ K_c = HW_{k,c},\ V_c = HW_{v,c},\ Q_r = PW_{q,r},\ K_r = PW_{k,r} $$ $$ \tilde{A}_{i,j} = \underbrace{Q_i^c{K_j^c}^T}_{(a)content-to-content} + \underbrace{Q_i^c{K_{\delta(i,j)}^r}^T}_{(b)content-to-position} + \underbrace{K_j^c{Q_{\delta(j,i)}^r}^T}_{(c)position-to-content} $$ $$ H_o = softmax(\frac{\tilde{A}}{\sqrt{3d}})V_c $$

说实话，第三个分量不用 $\delta(i,j)$ 而是 $\delta(j,i)$ 我没有想明白为什么，论文中关于它的解释只有一句话：This is because for a given position i, position-to-content computes the attention weight of the key content at j with respect to the query position at i, thus the relative distance is $\delta(j,i)$. $\delta(i,j)$ 的计算公式如下： $$ \delta(i,j) = \begin{cases} 0 & \text{for $i-j\leq-k$} \\ 2k-1 & \text{for $i-j\geq k$} \\ i-j+k & \text{others.} \end{cases}$$

除此之外，具体实现的时候，作者并没有像[1]中一样存储了所有的相对位置编码（需要 $O(N^2d)$ 的空间复杂度），而是只是存储了上述的 $P \in \mathbb{R}^{2k \times d}$，也可以理解为存储了 $K^r \in \mathbb{R}^{2k \times d}$ 和 $Q_r \in \mathbb{R}^{2k \times d} $，由于最后的 $\delta(i,j)$ 函数计算的值域其实是 [0, 2k-1] 的，因此在矩阵乘法计算完成后，通过索引取相应位置的结果即可，从而空间复杂度降低到了 $O(kd)$。

2. Enhanced Mask Decoder(EMD)

在这一部分作者首先通过一个例子: "a new store opened beside the new mall." 引出主旨，我们让预训练模型通过 MLM 去预测单词 “store” 和 “mall”，但这两个单词的部分上下文信息（这里指相对位置和周围词）是相同的，比如都位于“new”这个单词的后面且与其相对位置相同，因此这就给模型区分两个单词造成了困难，但这句话的主语是“store”而不是“mall”，因此作者认为绝对位置信息也是很重要的。但在 BERT 中，绝对位置信息是加在序列的输入向量中的，在这里我们已经修改成了相对位置信息，那么还怎么把绝对位置信息加入进去呢？既然我们这里的绝对位置信息是为了让 MLM 更好的预测被 mask 掉的单词，那作者就将绝对位置信息加在了最后 softmax 之前（准确的说是之前的解码器的输入上）。

除了绝对位置信息之外，作者还认为对于特定的下游任务，我们一般会在预训练模型后面加一个关于特定任务的解码器，但是预训练阶段的 MLM 却只有一个softmax层（除了前面那一些 dense 和 LN），这难免会造成一些不匹配，因此将原来的只有 softmax 层变成了两层的 transformer encoder layer + softmax。如下图所示：

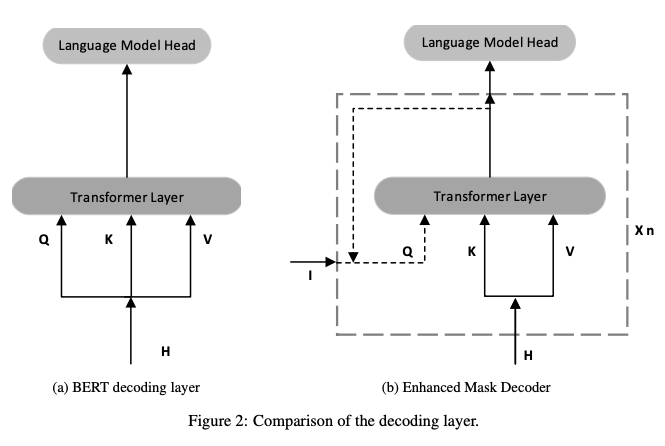
刚看到这幅图可能有点晕，（a）代表的就是原始 BERT 的 MLM 的结构，可以看到从 BERT 的最后一层 Transformer encoder layer 出来的向量直接输入至 MLM 的解码器；而（b）表示的就是论文修改后的 EMD，其中 I 可以代表多种信息：1.绝对位置信息；2.绝对位置信息+隐层向量；3.隐层向量（前一层的输出）。$x_n$ 代表单元循环 n 次，所以当 n = 1，I = H 时，EMD 其实就和 BERT 的解码器是一样的。并且作者提到，在 DeBERTa 中，他们将 n 设置为了 2，并且 n 个单元的参数是共享的。

但到这里我还是很疑惑的，那作为预训练模型的那一些 Transformer encoder layer 有多少层呢？加上这个 EMD，不会造成参数量的增长吗？这些问题在论文开源的代码中我找到了答案。

def emd_context_layer(self, encoder_layers, z_states, attention_mask, encoder, target_ids, input_ids, input_mask, relative_pos=None):
    if attention_mask.dim()<=2:
        extended_attention_mask = attention_mask.unsqueeze(1).unsqueeze(2)
        att_mask = extended_attention_mask.byte()
        attention_mask = att_mask*att_mask.squeeze(-2).unsqueeze(-1)
    elif attention_mask.dim()==3:
        attention_mask = attention_mask.unsqueeze(1)
    target_mask = target_ids>0
    # 取 deberta 的倒数第二层的隐层输出向量
    hidden_states = encoder_layers[-2]
    # 从这里开始 EMD 的计算
    if not self.position_biased_input: 
        # EMD 的 transformer encoder layer 有两个 \
        # 但都是用的 deberta 的最后一层的 encoder layer，因此论文中说参数共享
        layers = [encoder.layer[-1] for _ in range(2)]
        # `z_status`最开始传入进来的是绝对位置信息，现在加上上一层的输出
        z_states +=  hidden_states
        query_states = z_states
        query_mask = attention_mask
        outputs = []
        rel_embeddings = encoder.get_rel_embedding()

        # 注意只有 EMD 的第一层 layer 才传入了绝对位置信息 \
        # 第二层的 layer 传入的是上一层的输出
        for layer in layers:
            # TODO: pass relative pos ids
            output = layer(hidden_states, query_mask, return_att=False, query_states = query_states, relative_pos=relative_pos, rel_embeddings = rel_embeddings)
            query_states = output
            outputs.append(query_states)
    else:
        outputs = [encoder_layers[-1]]
    
    _mask_index = (target_ids>0).view(-1).nonzero().view(-1)
    def flatten_states(q_states):
        q_states = q_states.view((-1, q_states.size(-1)))
        q_states = q_states.index_select(0, _mask_index)
        return q_states

    return [flatten_states(q) for q in outputs]

根据源码，我们可以大致推断出，对标一个具有 12 层 Transformer encoder layer 的 BERT，DeBERTa 的 Transformer encoder layer 有 11 层，但有额外的 1 层 用于 EMD，并且复用这 1 层一次，相当于循环两次该层，最后整个 DeBERTa 的参数量其实还是 12 层，参数规模与 BERT 一致，不得不说确实巧妙。其他关于 EMD 的输入 I 的问题均在代码中以中文注释标注出来了。

四、Scale Invariant Fine-tuning

这部分主要介绍了一种用于 Fine-tuning 阶段的训练技巧，借鉴于虚拟对抗训练算法（virtual adversarial training algorithm），论文提出了一种规模不变微调（Scale Invariant Fine-tuning，SiFT）。虚拟对抗训练是一种提高模型泛化能力的正则化方法，它通过提高模型对对抗性示例的鲁棒性来实现，对抗性示例是通过对输入进行小幅扰动而创建的。

作者指出，对于 NLP 任务，扰动应用于词嵌入而不是原始词序列。然而，嵌入向量的取值范围（范数）在不同的词和模型之间有所不同。对于具有数十亿个参数的更大模型，方差会变得更大，从而导致对抗性训练的一些不稳定性。而对于 SiFT 的对于 VAT 的改进就一句话描述：“applying the perturbations to the normalized word embeddings”，也就是说在经过标准化后的 word embedding 上添加随机扰动，从而就可以限定扰动的”方差“的值的范围不会太大，也不会太小^[3]。

但 SiFT 算法只应用到了 DeBERTa1.5B 这个模型上面，我们直接看结果。

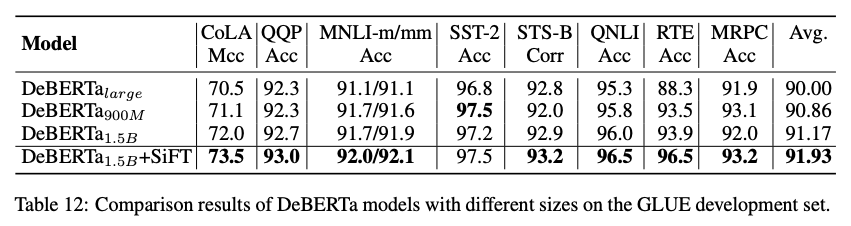
可以看到，在 DeBERTa1.5B 上加入 SiFT 后，性能有了进一步的提升。

五、实验结果

这部分的消融实验做的挺充分的，累了，就不贴图了，大伙自己去原文看吧…

六、参考文献

[1] Shaw P, Uszkoreit J, Vaswani A. Self-Attention with Relative Position Representations[C]//Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers). 2018: 464-468.
[2] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Advances in neural information processing systems. 2017: 5998-6008.
[3] https://zhuanlan.zhihu.com/p/395086745