Transformer 解读

Deep Learning 32 分钟 读完 (约 4819 字)

Transformer 是 Google Brain 发表在 NIPS2017 的论文《Attention is all you need》中提出的模型，随着深度学习的火热，基于Transformer的预训练模型已经席卷 NLP 领域，足见Transformer的重要性。 本文将按照这篇论文的顺序并结合一定的代码进行解读，但会调整论文中某些部分的顺序。

0. 初次见面

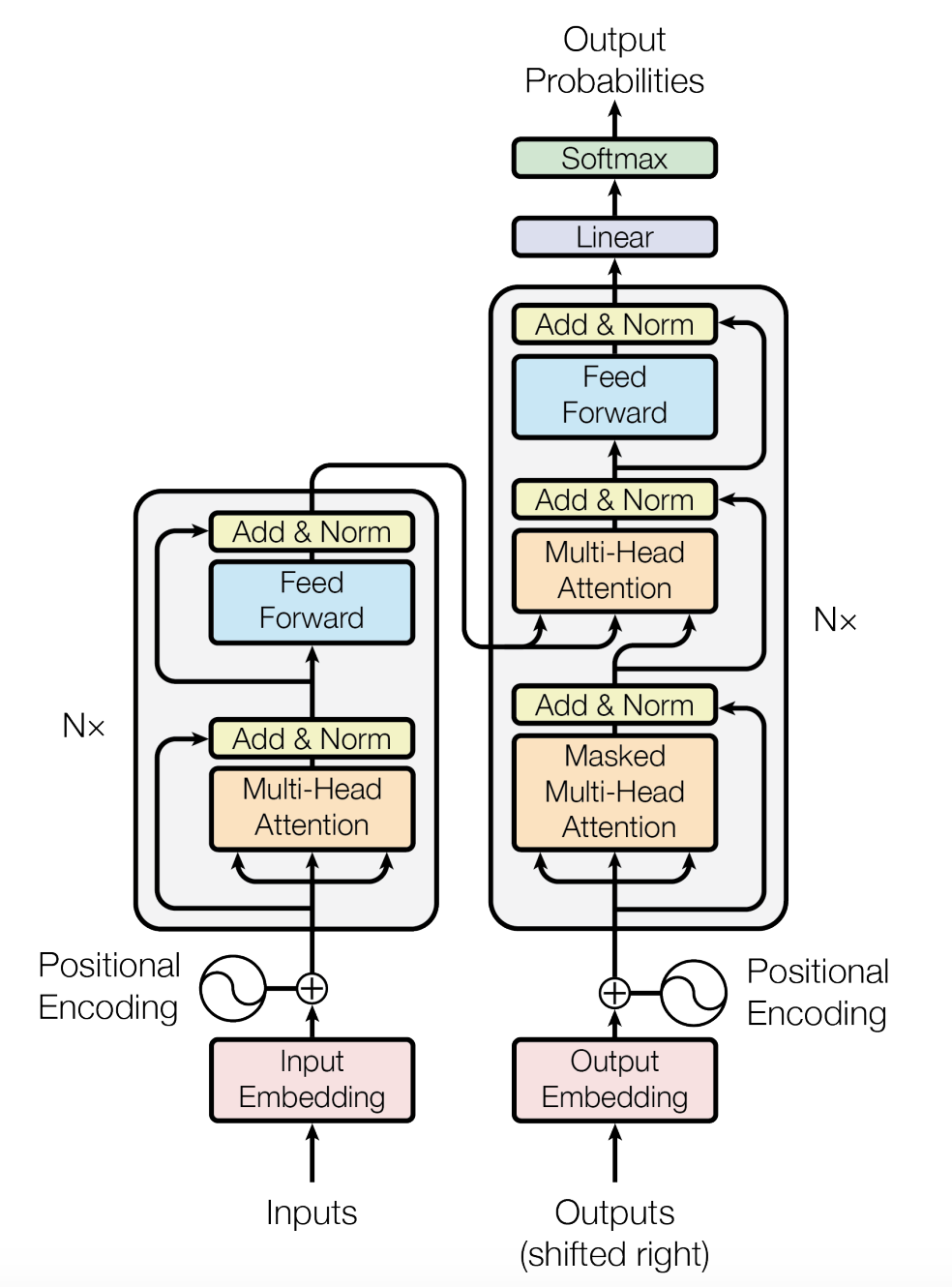
transformer.png

我们可以从上图看到Transformer的总体结构，可以发现，他与传统的神经网络如 RNN（LSTM、GRU）有着显著的不同。循环神经网络如RNN的训练是迭代的、串行的，必须要等到前一个 step 计算完成才会去计算下一个 step ，也就是后一个单元的运算依赖于前一个单元的输出，在这里不得不再次指出 RNN 的两个缺陷：

  • 时间片的计算依赖问题，无法并行计算
  • 顺序计算的过程中信息会丢失，尽管 LSTM 等门机制在一定程度上缓解了长期依赖的问题，但在对于特别长期的依赖现象上，LSTM 依旧无能为力。

而 Transformer 则完全摒弃了 RNN，转而采用自注意力机制（Self Attention Mechanism）来绘制输入和输出之间的全局依赖关系。

总体上，Transformer主要分为 Encoder 和 Decoder 两个部分，前者负责把输入的文本序列转换成隐藏层表示，也就是编码成具有上下文表示的中间向量，之后通过解码器（Decoder）再把隐藏层表示解码成文本序列。

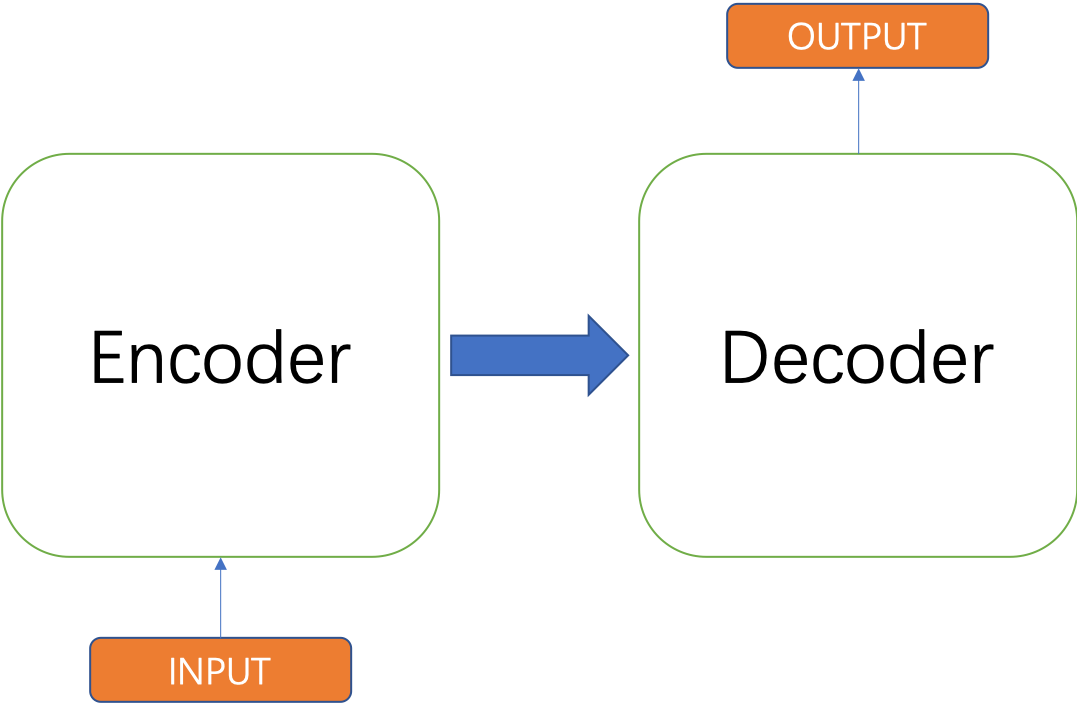
Encoder-Decoder

而 Encoder 和 Decoder 均是由第一张图中的 Encoder Layer 和 Decoder Layer 分别堆叠而成，原论文中使用 Stacks 来形容。Encoder Layer 和 Decoder Layer 又长得十分相似，主要分为以下几个部分，本文也按照如下顺序展开。

  • Model Architecture
  • Positional Encoding
  • Scaled Dot-Product Attention
  • Multi-Head Attention
  • Position-wise Feed-Forward Networks
  • Masked Multi-Head Attention
  • Transformer Encoder 一览
  • Transformer Decoder 一览
  • The END

1. Model Architecture

1.1 Positional Encoding

前面提到，Transformer中没有递归和卷积操作，因此模型缺少了序列的顺序信息，为了让模型能够利用序列的顺序，必须加入一些序列中的有关于相对或绝对位置的信息。论文中最终使用了 "Positional Encoding"，并将其加入到 "the bottom of the encoder and decoder stacks"，即在 Word Embedding 处添加了一个位置嵌入，因此这个位置嵌入的维度是和词（字）向量的维度相同的。

论文中使用了 sin 和 cos 函数的线形变换来作为序列顺序的位置信息： $$ PE(pos, 2i) = sin(pos/1000^{2i/d_{model}}) $$ $$ PE(pos, 2i+1) = cos(pos/1000^{2i/d_{model}}) $$

其中，pos 指当前字位于序列的中的位置，取值范围为 [0, max_sequence_length-1]；而 i 指的是维度，前面提到，位置嵌入的维度是和字向量的维度相同的，对于偶数维度，采用 sin，而对于奇数维度，采用 cos 函数。$d_{model}$即位置嵌入与字向量维度数。

位置嵌入在 $d_{model}$ 上随着维度序号的增大，周期变化越来越慢，从最初的 $2\pi$ 变化至 $10000*2\pi$，而每一个字或单词都会在整个 $d_{model}$ 维度上获得不同周期的 sin 与 cos 函数的取值组合，最终以此作为序列的位置信息加入至模型当中。 位置向量在这里有两个作用：

  • 决定当前词的位置
  • 计算在一个句子中不同的词之间的距离

我们实际画一下位置嵌入的图像，纵向观察下图，可以发现随着 $d_{model}$ 的序号的增大，位置嵌入的变化越来越平缓。



1.2 Scaled Dot-Product Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output,
where the query, keys, values, and output are all vectors.

上述这句话出自原论文，也就是说，对于 Self-Attention，定义了一个query、key 和 values，而剩下的就是他们三个之间的互动了。这里我们分别将其表示为Q、K、V。直接上原文图！

transformer.png

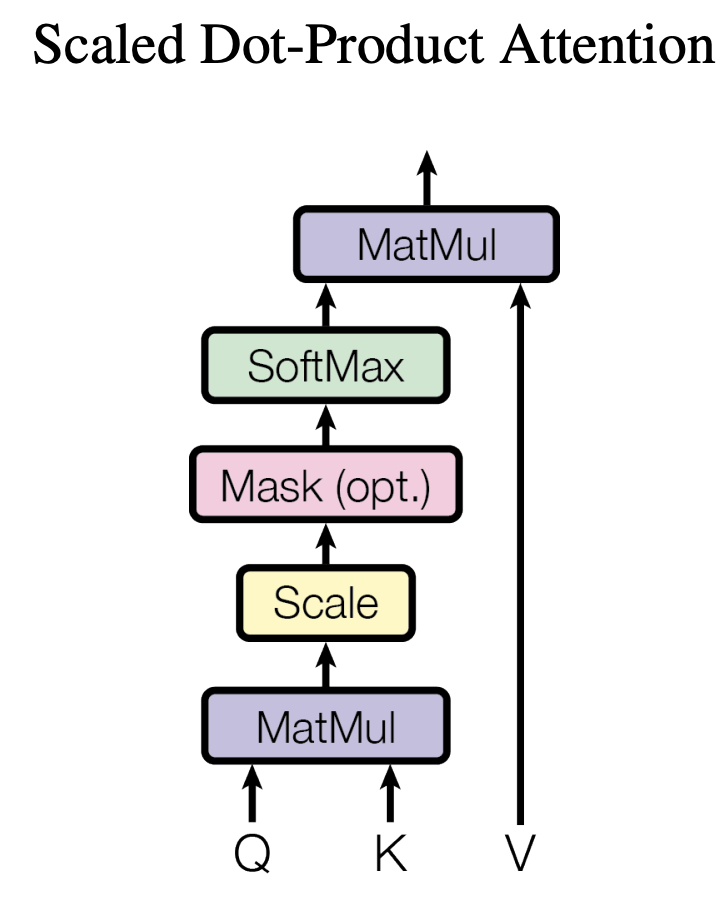
通过上图可以看到，这个 Scaled Dot-Product Attention 主要进行以下几个操作

  • a. 将 Q 和 K 进行了矩阵乘法（注意 K 需要被转置）。
  • b. 对 a 中结果进行了Scaled操作，其实也就是除以了 $\sqrt{d_{k}}$ 。
  • c. 将 b 的结果执行了mask操作，这一步是为了防止下一步的 softmax 概率化了 Padding 等无用位置。
  • d. 最后将 c 的结果乘以矩阵 V 即得到最后结果。

总结下来，就是一个公式：$$ Attention(Q, K, V) = softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V $$
而至于为什么需要 Scaled，也就是为什么要执行 b 操作，原文是这么解释的： We suspect that for large values of
$d_{k}$, the dot products grow large in magnitude, pushing the softmax function into regions where it has
extremely small gradients. 也就是说，作者认为当维度很大时，点积的结果会很大，会导致 Softmax 的梯度很小，为了减轻这个影响，对点积进行缩放。当然，假设 Q 和 K 的均值为 0，方差为 1。它们的矩阵乘积将有均值为 0，方差为 $d_{k}$，因此使用$d_{k}$的平方根用于缩放。

关于为什么要 Scaled 的数学层面的理解请看 这里

不多说，放代码！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
'''
假设 d_k 已定义
假定 d_q == d_k == d_v
'''
class ScaledDotProductAttention(nn.Module):
    def __init__(self):
        super(ScaledDotProductAttention, self).__init__()
    
    def forward(self, Q, K, V, attn_mask):
        '''
        Q: [batch_size, n_heads, len_q, d_k]
        K: [batch_size, n_heads, len_k, d_k]
        V: [batch_size, n_heads, len_v(=len_k), d_v]
        attn_mask: [batch_size, n_heads, seq_len, seq_len]
        '''
        scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k)
        scores.masked_fill_(attn_mask, -1e9)
        
        attn = nn.Softmax(dim = -1)(scores)
        context = torch.matmul(attn, V) # [batch_size, n_heads, len_q, d_v]
        return context, attn

在上述代码的第17行，我们可以发现执行了一个 Mask 操作，将 scores 矩阵的对应位置变成了 -1e9，这里解释一下：因为我们通常训练是一个batch送入模型的，因此需要保证这个batch中的例如每一句话需要等长，所以需要给每一句话 Padding 到设定的最大长度，而用于 Padding 的占位符是没有任何文本意义的，如果不加以操作就将 scores 进行 Softmax，就会让没有意义的 Padding 部分参与了 Softmax 运算，Softmax函数为 $\sigma(z_{i}) = \frac{e^{z_{i}}}{\sum_{j=1}^{K}e^{z_{i}}}$，我们可以透过公式看到，$e^{0}$ 是有值的。为了解决这个问题，就需要给原先 Padding 的部分加上一个很大的负数偏置，使得 Padding 位置经过 Softmax 为 0。

1.3 Multi-Head Attention

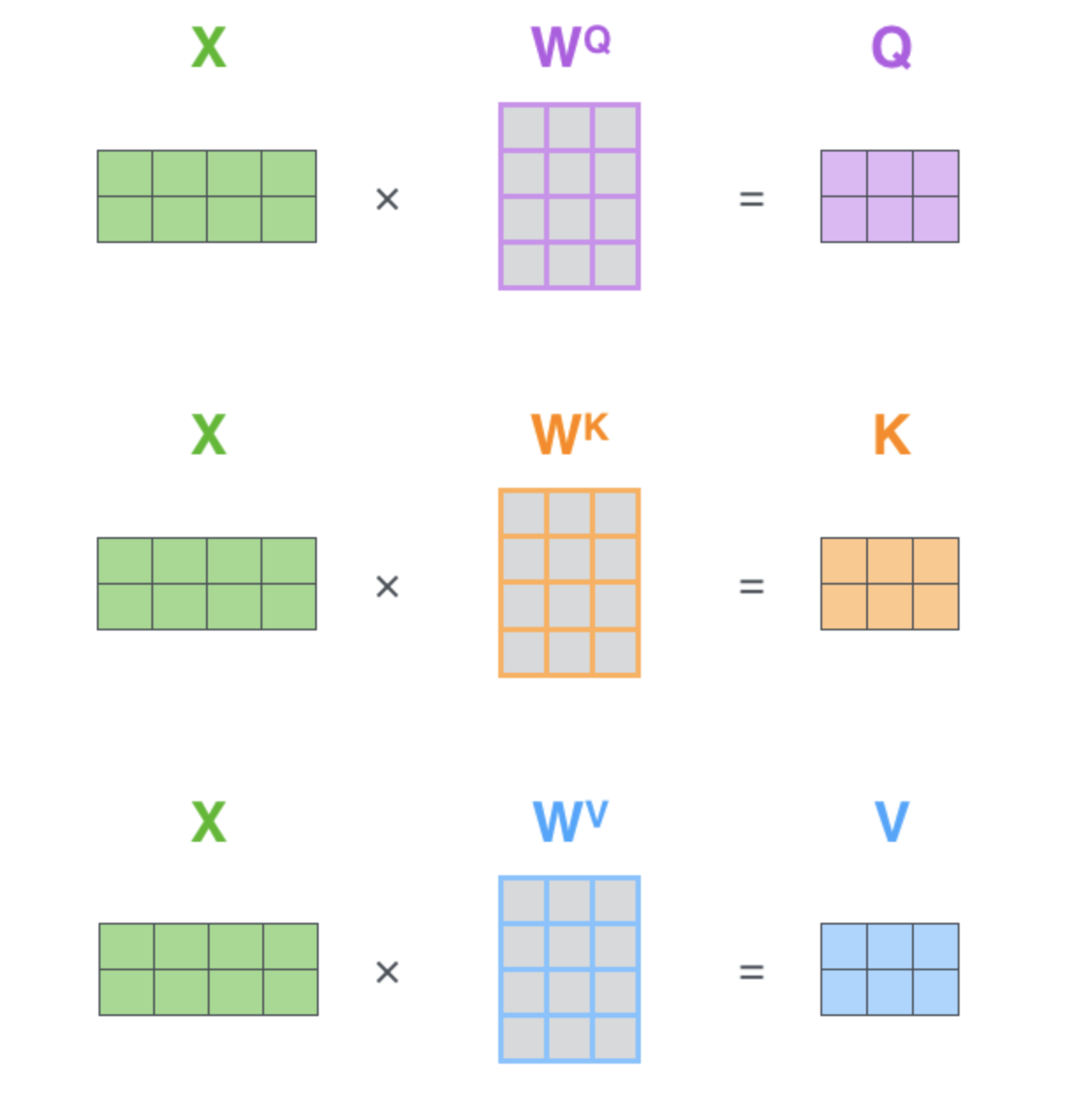
那 Q、K、V 又是什么呢？矩阵？我知道它是一个个的矩阵，它们三个是怎么来的呢？其实它们三个都是通过将 Input Embedding（当然还有可能是Output Embedding，这里默认已经加上了位置嵌入，普遍而言，就是进入到这一模块的输入）线形变换得到的一个个的矩阵。我们在这一模块，初始化三个 nn.Linear 层，分别为$W^{Q}, W^{K}, W^{V}$，即可将输入 x 分别线性变换成 Q、K、V，如下图所示：

QKV

那 Multi-Head 又是什么意思呢，翻译成中文，多头？其实很简单，之前我们定义的一组 Q、K、V 可以让一个词关注到与他相关的词，我们现在通过定义多组 Q、K、V，让它们分别去关注不同的上下文信息，可以理解为让我们的模型透过不同的角度去看数据。计算的方式并没有变化。

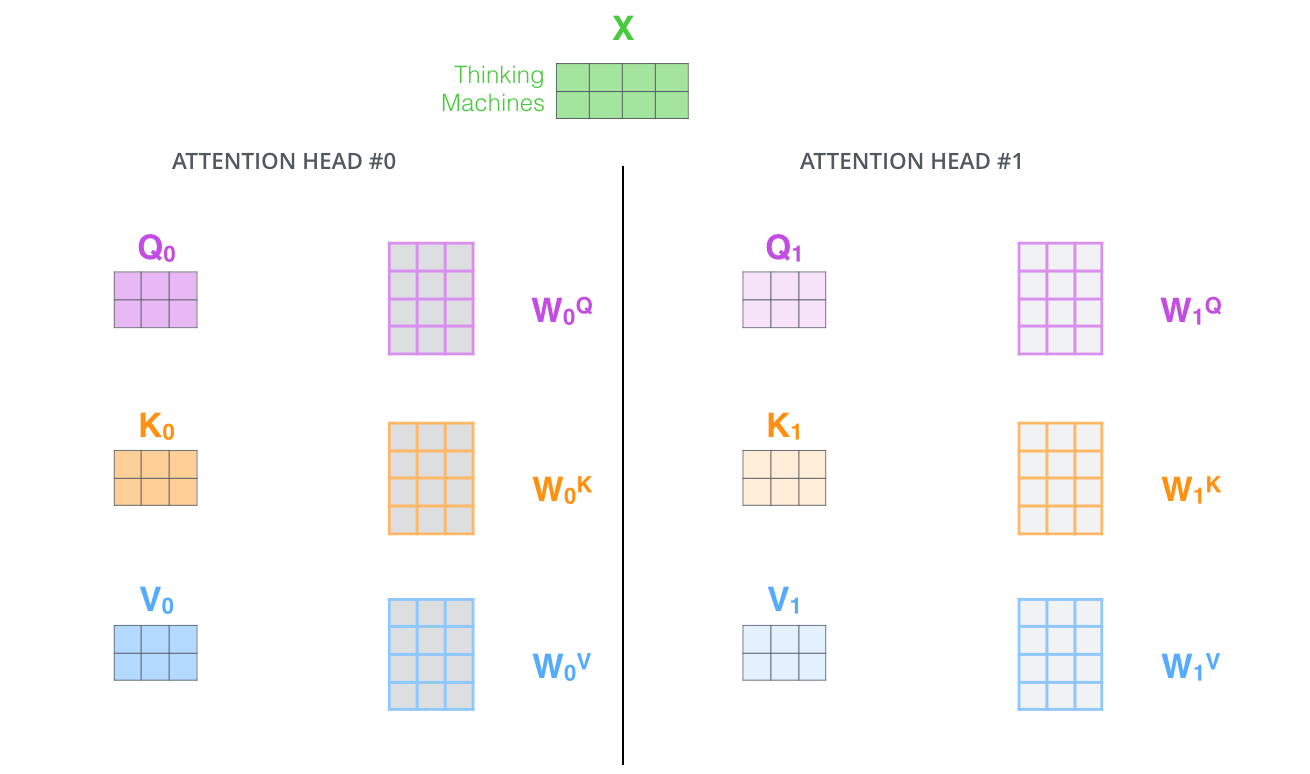
multiHead

最后将每个 Head 得到的 context 向量 Concat 到一起，即得到了我们最后需要的结果。MultiHead Attention 整体结构图如下所示：

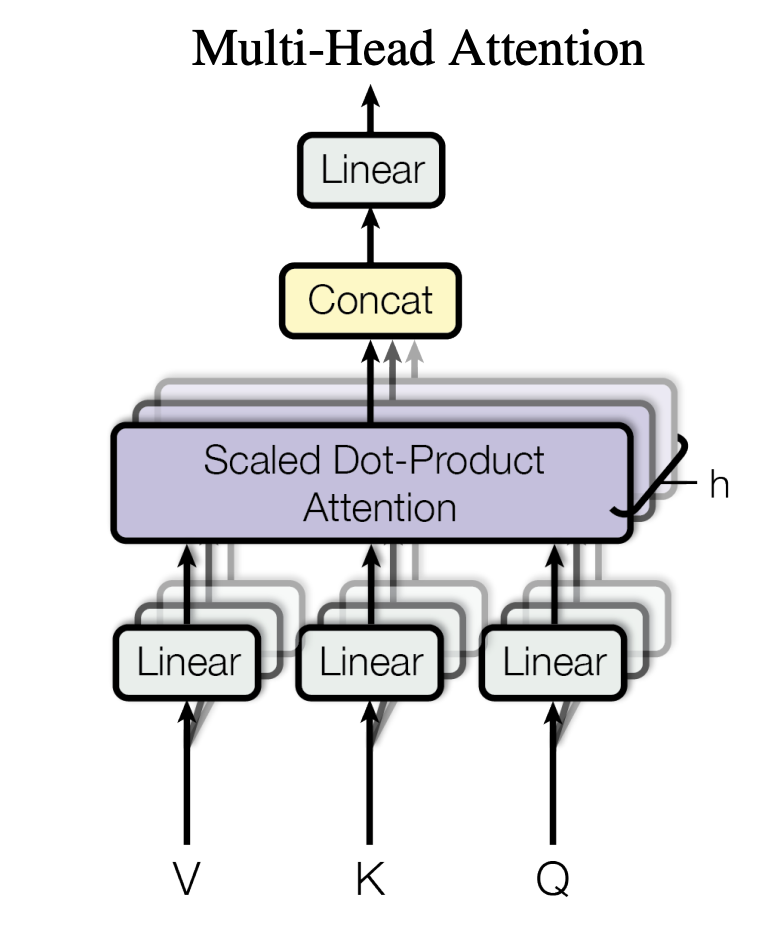
multiHeadAttn

在这一部分展示代码之前，我们需要再展开说一下残差连接和 Layer Normalization。

  • 残差连接

残差网络是在2015年《Deep residual learning for image recognition》中提出的。其具体操作很简单，在我们的实例中，就是将模块前的输入加到经过模块计算后的结果上，再输送至下一神经单元中。也就是 $$ NEXT = X_{embedding} + SelfAttention(Q, K, V) $$

  • Layer Normalization

LN是啥？还有BN？一张图搞清楚！

BN_LN

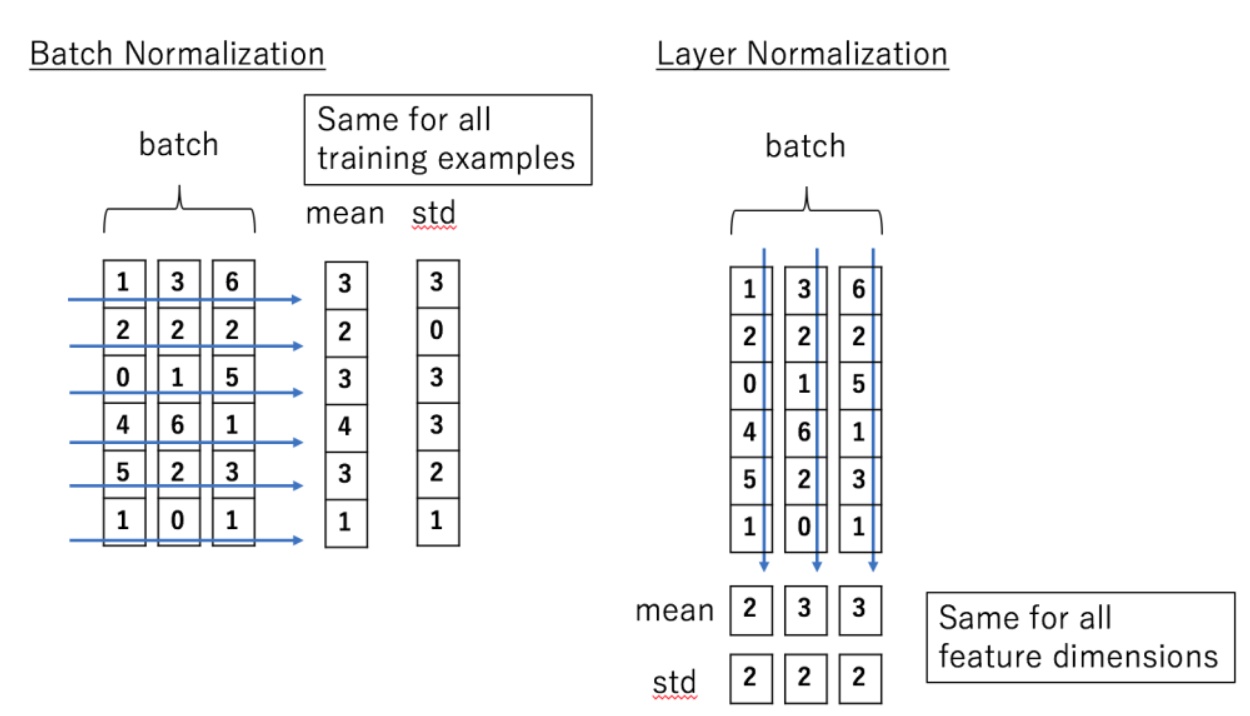
Layer Normalization 的作用就是把神经网络隐藏层归一化为标准正态分布，以便于起到加快训练速度，加速收敛的作用。如何变成标准正态分布，相信大家在概率课或者数理统计课上早已经学过了。

继续，上代码！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class MultiHeadAttention(nn.Module):
    def __init__(self):
        super(MultiHeadAttention, self).__init__()
        self.W_Q = nn.Linear(d_model, d_k * n_heads, bias = False)
        self.W_K = nn.Linear(d_model, d_k * n_heads, bias = False)
        self.W_V = nn.Linear(d_model, d_v * n_heads, bias = False)
        self.fc = nn.Linear(n_heads * d_v, d_model, bias = False)
    
    def forward(self, input_Q, input_K, input_V, attn_mask):
        '''
        input_Q: [batch_size, len_q, d_model]
        input_K: [batch_size, len_k, d_model]
        input_V: [batch_size, len_v(=len_k), d_model]
        attn_mask: [batch_size, seq_len, seq_len]
        '''
        residual, batch_size = input_Q, input_Q.size(0)
        # (B, S, D) -proj-> (B, S, D_new) -split-> (B, S, H, W) -trans-> (B, H, S, W)
        Q = self.W_Q(input_Q).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # Q: [batch_size, n_heads, len_q, d_k]
        K = self.W_K(input_K).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # K: [batch_size, n_heads, len_k, d_k]
        V = self.W_V(input_V).view(batch_size, -1, n_heads, d_v).transpose(1,2)  # V: [batch_size, n_heads, len_v(=len_k), d_v]

        attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1) # attn_mask : [batch_size, n_heads, seq_len, seq_len]

        # context: [batch_size, n_heads, len_q, d_v], attn: [batch_size, n_heads, len_q, len_k]
        context, attn = ScaledDotProductAttention()(Q, K, V, attn_mask)
        context = context.transpose(1, 2).reshape(batch_size, -1, n_heads * d_v) # context: [batch_size, len_q, n_heads * d_v]
        output = self.fc(context) # [batch_size, len_q, d_model]
        return nn.LayerNorm(d_model).cuda()(output + residual), attn

1.4 Position-wise Feed-Forward Networks

这一部分就显得比较简单了，总共包含两个线形层外加一个ReLU激活层，具体公式如下所示： $$ FFN(x) = max(0, xW_{1} + b_{1})W_{2} + b_{2} $$ 首先上一阶段的输出做一个线形变换，再经过一个ReLU激活，最后再经过一个线形变换。这就是这一部分的所有操作，具体代码如下（在这里将后续的残差连接与LN也放在一起实现）： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class PoswiseFeedForwardNet(nn.Module):
    def __init__(self):
        super(PoswiseFeedForwardNet, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(d_model, d_ff, bias=False),
            nn.ReLU(),
            nn.Linear(d_ff, d_model, bias=False)
        )
    def forward(self, inputs):
        '''
        inputs: [batch_size, seq_len, d_model]
        '''
        residual = inputs
        output = self.fc(inputs)
        return nn.LayerNorm(d_model).cuda()(output + residual) # [batch_size, seq_len, d_model]

这部分最后，上一个 Encoder Layer模块的细节图：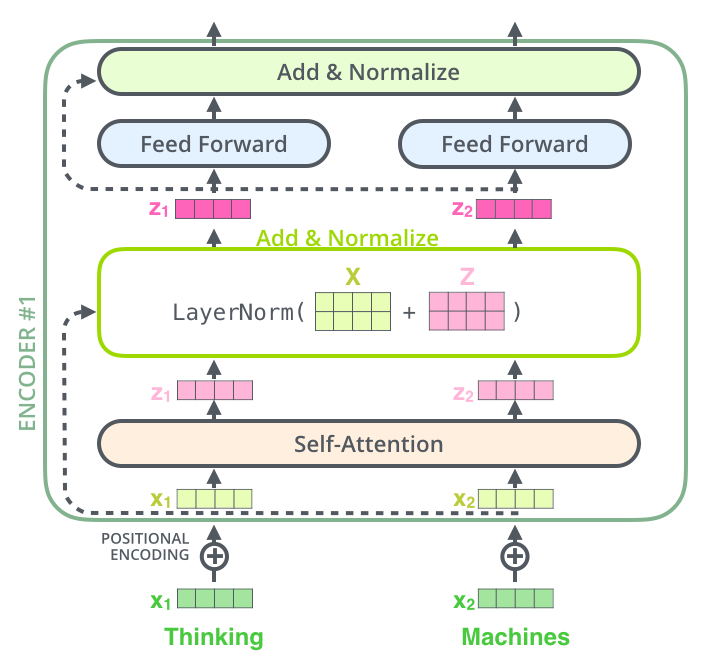
encoderLayer

1.5 Masked Multi-Head Attention

整个 Transformer 模型的子单元结构只剩下 Masked Multi-Head Attention 这一个部分了，细心的朋友们可以发现，这个单元只有在 Decoder Layer 中存在，在 Encoder Layer 中并没有这个结构单元。那我们不难猜出这个部分设置的目的是什么。

在传统的 Seq2Seq 中，Decoder 部分使用的一般是 RNN，所以，在训练过程中 t 时间步的词，模型是无法看到大于 t 时间步的词的，同时，我们本来也是不能将所要预测的结果直接暴露给模型的。因此，如果 Decoder Layer 部分继续像 Encoder Layer 的 Self-Attention 一样，就会在训练过程中将所有的正确答案告诉了模型，所以我们需要对 Decoder Layer 的输入部分进行一定的处理，也就是 Mask 。

这波很关键啊，我又要祭出这幅图了！

scaledDotProductAttn.png

在 1.2 部分，我们提到，图中的 Mask 部分是为了防止 Padding 部分影响了 Softmax 操作，那如果我们在这部分的基础上继续添加一个 Mask ，使得前序单词无法捕捉到后续单词的关系，那我们的 Masked Multi-Head Attention 也就完成了。可怎么做呢？

首先生成一个下三角全0，上三角全为负无穷（-1e9）的矩阵，然后将它和 Scaled 后的矩阵相加即可。如下图中的例子所示：

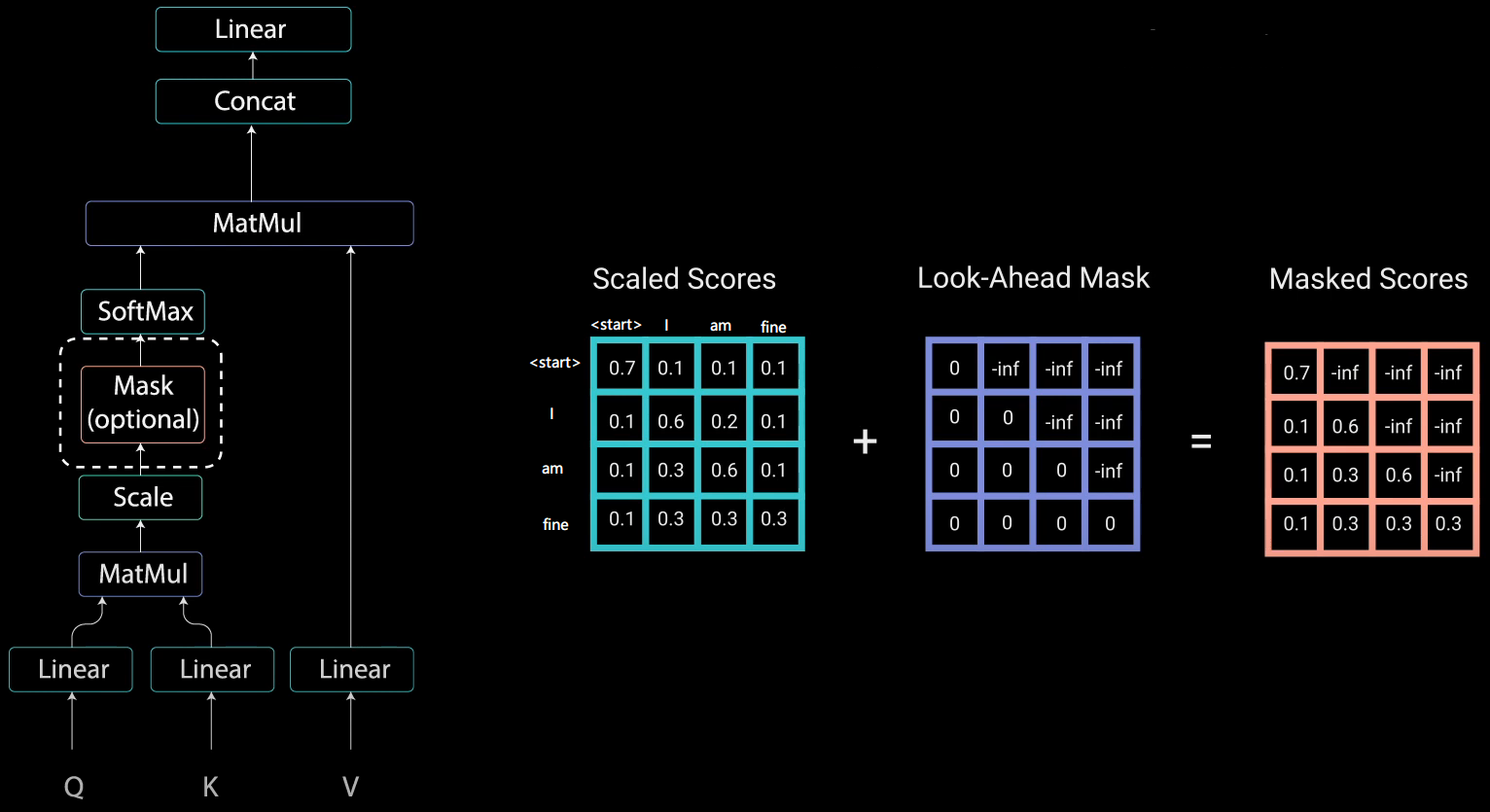
maskAttn1.png

这样的矩阵经过 Softmax 后，负无穷处就会变为 0，而剩下的部分，可以看到，只有后续的单词才有与其前面单词的注意力权重。例如: “am” 这个单词只有与 “start” 和 “I” 以及其自身的权重值，它与其后续的 “fine” 的权重值为 0。

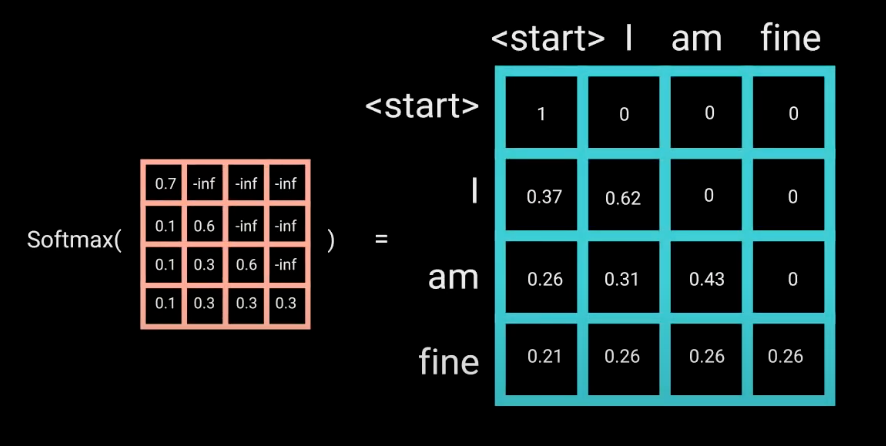
maskAttn2.png

所以总结一下，Masked Multi-Head Attention 就是在 Multi-Head Attention 的基础上在 Scaled 之前多加了一个 Mask 操作。

2. Transformer Encoder 一览

一个 Encoder 会包含 n 个 Encoder Layer，在这篇论文中，n = 6，而一个 Encoder Layer 又由上述几个模块组成的。

  1. 字向量与位置编码
    $$ X = Embedding(X) + Positional_Encoding $$

  2. Self-Attention
    $$ Q = Linear_{q}(X) = XW_{Q} $$
    $$ K = Linear_{k}(X) = XW_{K} $$
    $$ V = Linear_{v}(X) = XW_{V} $$
    $$ X_{attention} = softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V $$

  3. 残差连接与LN
    $$ X_{attention} = X + X_{attention} $$
    $$ X_{attention} = LayerNorm(X_{attention}) $$

  4. Feed-Forward
    $$ X_{hidden} = Linear(ReLU(Linear(X_{attention}))) = max(0, X_{attention}W_{1} + b_{1})W_{2} + b_{2} $$

  5. 残差连接与LN
    $$ X_{hidden} = X_{attention} + X_{hidden} $$
    $$ X_{hidden} = LayerNorm(X_{hidden}) $$

Show The Code!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class EncoderLayer(nn.Module):
    def __init__(self):
        super(EncoderLayer, self).__init__()
        self.enc_self_attn = MultiHeadAttention()
        self.pos_ffn = PoswiseFeedForwardNet()

    def forward(self, enc_inputs, enc_self_attn_mask):
        '''
        enc_inputs: [batch_size, src_len, d_model]
        enc_self_attn_mask: [batch_size, src_len, src_len]
        '''
        # enc_outputs: [batch_size, src_len, d_model], attn: [batch_size, n_heads, src_len, src_len]
        enc_outputs, attn = self.enc_self_attn(enc_inputs, enc_inputs, enc_inputs, enc_self_attn_mask) # enc_inputs to same Q,K,V
        enc_outputs = self.pos_ffn(enc_outputs) # enc_outputs: [batch_size, src_len, d_model]
        return enc_outputs, attn

class Encoder(nn.Module):
    def __init__(self):
        super(Encoder, self).__init__()
        self.src_emb = nn.Embedding(src_vocab_size, d_model)
        self.pos_emb = PositionalEncoding(d_model)
        self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)])

    def forward(self, enc_inputs):
        '''
        enc_inputs: [batch_size, src_len]
        '''
        enc_outputs = self.src_emb(enc_inputs) # [batch_size, src_len, d_model]
        enc_outputs = self.pos_emb(enc_outputs.transpose(0, 1)).transpose(0, 1) # [batch_size, src_len, d_model]
        enc_self_attn_mask = get_attn_pad_mask(enc_inputs, enc_inputs) # [batch_size, src_len, src_len]
        enc_self_attns = []
        for layer in self.layers:
            # enc_outputs: [batch_size, src_len, d_model], enc_self_attn: [batch_size, n_heads, src_len, src_len]
            enc_outputs, enc_self_attn = layer(enc_outputs, enc_self_attn_mask)
            enc_self_attns.append(enc_self_attn)
        return enc_outputs, enc_self_attns

3. Transformer Decoder 一览

我们先上图，毕竟 Decoder Layer 部分还是比 Encoder Layer部分多了一点东西的！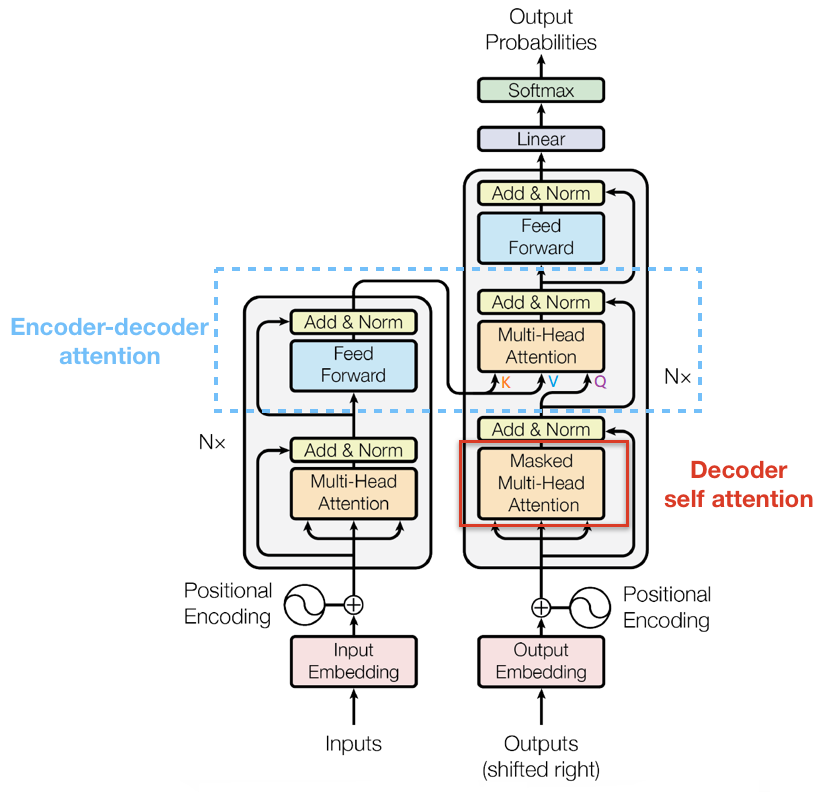
transformer.png

我们把用红线框起来的部分叫做 Decoder self attention，而用蓝虚线框起来的部分区分为 Encoder-Decoder attention。在前面我们已经介绍过了 Decoder self attention 部分，它仅仅是多了一个上三角矩阵用于mask掉未知的权重信息；而后者与前述的 Self-Attention 并无不同，唯一的区别在于其中产生 Q 的输入来自于其前面的 Decoder self attention 部分，而 产生 K 和 V 的输入来自于最后一个 Encoder Layer 的输出，也就是整个 Encoder 的输出。

Show The Code!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class DecoderLayer(nn.Module):
    def __init__(self):
        super(DecoderLayer, self).__init__()
        self.dec_self_attn = MultiHeadAttention()
        self.dec_enc_attn = MultiHeadAttention()
        self.pos_ffn = PoswiseFeedForwardNet()

    def forward(self, dec_inputs, enc_outputs, dec_self_attn_mask, dec_enc_attn_mask):
        '''
        dec_inputs: [batch_size, tgt_len, d_model]
        enc_outputs: [batch_size, src_len, d_model]
        dec_self_attn_mask: [batch_size, tgt_len, tgt_len]
        dec_enc_attn_mask: [batch_size, tgt_len, src_len]
        '''
        # dec_outputs: [batch_size, tgt_len, d_model], dec_self_attn: [batch_size, n_heads, tgt_len, tgt_len]
        dec_outputs, dec_self_attn = self.dec_self_attn(dec_inputs, dec_inputs, dec_inputs, dec_self_attn_mask)
        # dec_outputs: [batch_size, tgt_len, d_model], dec_enc_attn: [batch_size, h_heads, tgt_len, src_len]
        dec_outputs, dec_enc_attn = self.dec_enc_attn(dec_outputs, enc_outputs, enc_outputs, dec_enc_attn_mask)
        dec_outputs = self.pos_ffn(dec_outputs) # [batch_size, tgt_len, d_model]
        return dec_outputs, dec_self_attn, dec_enc_attn

class Decoder(nn.Module):
    def __init__(self):
        super(Decoder, self).__init__()
        self.tgt_emb = nn.Embedding(tgt_vocab_size, d_model)
        self.pos_emb = PositionalEncoding(d_model)
        self.layers = nn.ModuleList([DecoderLayer() for _ in range(n_layers)])

    def forward(self, dec_inputs, enc_inputs, enc_outputs):
        '''
        dec_inputs: [batch_size, tgt_len]
        enc_intpus: [batch_size, src_len]
        enc_outputs: [batsh_size, src_len, d_model]
        '''
        dec_outputs = self.tgt_emb(dec_inputs) # [batch_size, tgt_len, d_model]
        dec_outputs = self.pos_emb(dec_outputs.transpose(0, 1)).transpose(0, 1).cuda() # [batch_size, tgt_len, d_model]
        dec_self_attn_pad_mask = get_attn_pad_mask(dec_inputs, dec_inputs).cuda() # [batch_size, tgt_len, tgt_len]
        dec_self_attn_subsequence_mask = get_attn_subsequence_mask(dec_inputs).cuda() # [batch_size, tgt_len, tgt_len]
        dec_self_attn_mask = torch.gt((dec_self_attn_pad_mask + dec_self_attn_subsequence_mask), 0).cuda() # [batch_size, tgt_len, tgt_len]

        dec_enc_attn_mask = get_attn_pad_mask(dec_inputs, enc_inputs) # [batc_size, tgt_len, src_len]

        dec_self_attns, dec_enc_attns = [], []
        for layer in self.layers:
            # dec_outputs: [batch_size, tgt_len, d_model], dec_self_attn: [batch_size, n_heads, tgt_len, tgt_len], dec_enc_attn: [batch_size, h_heads, tgt_len, src_len]
            dec_outputs, dec_self_attn, dec_enc_attn = layer(dec_outputs, enc_outputs, dec_self_attn_mask, dec_enc_attn_mask)
            dec_self_attns.append(dec_self_attn)
            dec_enc_attns.append(dec_enc_attn)
        return dec_outputs, dec_self_attns, dec_enc_attns

4. The END

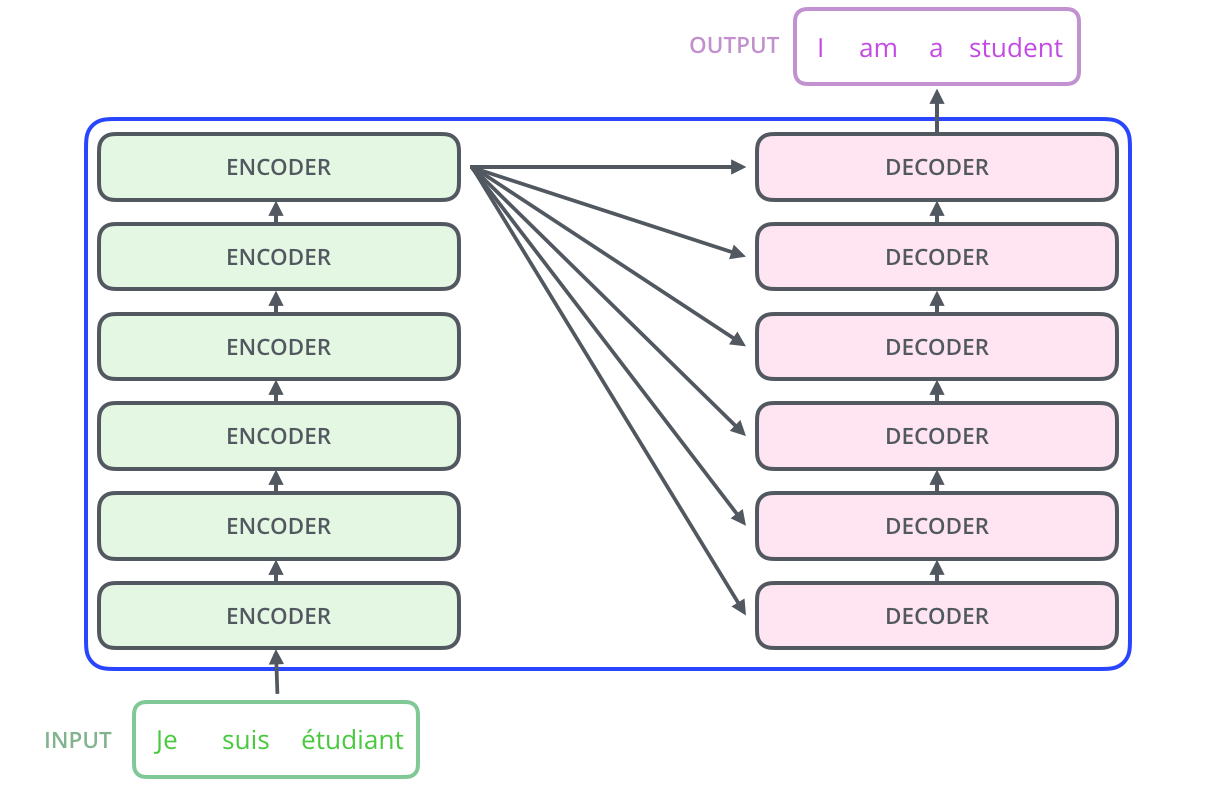
transformer.png

说来惭愧，最初去了解 Transformer 的时候，我总是有个疑惑，每个子单元结构我都知道了，但是它们是怎么级联起来的呢？看完上图，就会大致明白了，一定要注意是 Encoder 的最后一个 Layer 的输出会送入到 Decoder 的每一个 Layer 中，作为在 Encoder-Decoder attention 部分用于产生 K、V 矩阵。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Transformer(nn.Module):
    def __init__(self):
        super(Transformer, self).__init__()
        self.encoder = Encoder().cuda()
        self.decoder = Decoder().cuda()
        self.projection = nn.Linear(d_model, tgt_vocab_size, bias=False).cuda()
    def forward(self, enc_inputs, dec_inputs):
        '''
        enc_inputs: [batch_size, src_len]
        dec_inputs: [batch_size, tgt_len]
        '''
        # tensor to store decoder outputs
        # outputs = torch.zeros(batch_size, tgt_len, tgt_vocab_size).to(self.device)
        
        # enc_outputs: [batch_size, src_len, d_model], enc_self_attns: [n_layers, batch_size, n_heads, src_len, src_len]
        enc_outputs, enc_self_attns = self.encoder(enc_inputs)
        # dec_outpus: [batch_size, tgt_len, d_model], dec_self_attns: [n_layers, batch_size, n_heads, tgt_len, tgt_len], dec_enc_attn: [n_layers, batch_size, tgt_len, src_len]
        dec_outputs, dec_self_attns, dec_enc_attns = self.decoder(dec_inputs, enc_inputs, enc_outputs)
        dec_logits = self.projection(dec_outputs) # dec_logits: [batch_size, tgt_len, tgt_vocab_size]
        return dec_logits.view(-1, dec_logits.size(-1)), enc_self_attns, dec_self_attns, dec_enc_attns

完整代码：https://github.com/aestheticisma/iWantOffer/blob/main/Transformer/Transformer.ipynb

Reference

#Deep Learning
DeBERTa 论文解读 关于CUDA Toolkit安装失败解决措施总结（Ubuntu server 20.04.2）
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×