在看摘要的文章中突然发现拉格朗日乘数法这个名词,觉得很熟悉但不记得具体是什么了,简单记录以备遗忘。
看了wiki百科后,发现原来这个用来优化的方法在大二的一门课————《最优化方法》上学过,怪不得很熟悉,而且这貌似也是大一工数的知识…大四的小废物全部忘光了,该查缺补漏继续学习了…
一、简介(from wiki)
在数学中的最优化问题中,拉格朗日乘数法(以数学家约瑟夫·拉格朗日命名)是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数,即拉格朗日乘数,又称拉格朗日乘子,或拉氏乘子,它们是在转换后的方程,即约束方程中作为梯度(gradient)的线性组合中各个向量的系数。
比如,要求$f(x,y)$在$g(x,y) = c$时的最大值时,我们可以引入新变量拉格朗日乘数$\lambda$,这时我们只需要下列拉格朗日函数的极值:$\mathcal{L}(x,y,\lambda)=f(x,y)+\lambda \cdot {\Big (}g(x,y)-c{\Big )}$
更一般的,对含有n个变量和k个约束的情况,有:
$\mathcal{L}(x_{1},\ldots,x_{n},\lambda_{1},\ldots,\lambda_{k}) = f(x_{1},\ldots ,x_{n})-\sum \limits_{i=1}^{k}\lambda_{i}g_{i}(x_{1},\ldots,x_{n})$,
拉格朗日乘数法所得的极点会包含原问题的所有极值点,但并不保证每个极值点都是原问题的极值点。拉格朗日乘数法的正确性的证明牵涉到偏微分,全微分或链法。
二、证明
设函数$f(x,y)$在$A$处有极值$\kappa$,且在点$A$的邻域内连续。则在点$A$处有:
$f(x,y) = \kappa$
另有一常值函数
$g(x,y) = c$
两函数在$A$点处的全微分为:
$\mathrm{d}f=\dfrac{\partial{f}}{\partial{x}}\mathrm{d}x + \dfrac{\partial{f}}{\partial{y}}\mathrm{d}y = 0$
$\mathrm{d}g=\dfrac{\partial{g}}{\partial{x}}\mathrm{d}x + \dfrac{\partial{g}}{\partial{y}}\mathrm{d}y = 0$
由于齐次方程有非零解,也就是点$A$,所以该齐次方程的行列式为0,因此该线性方程组的系数成比例,有:
$\dfrac {\dfrac {\partial {f}}{\partial {x}}} {\dfrac {\partial {g}}{\partial {x}}} = \dfrac {\dfrac {\partial {f}}{\partial {y}}} {\dfrac {\partial {g}}{\partial {y}}} = -\lambda$
即:
$\dfrac{\partial{f}}{\partial{x}} + \lambda \dfrac{\partial{g}}{\partial{x}} = 0$
$\dfrac{\partial{f}}{\partial{y}} + \lambda \dfrac{\partial{g}}{\partial{y}} = 0$
将上二式分别乘以$\mathrm{d}x$和$\mathrm{d}y$,再相加并积分,得到一新函数
$\mathcal{L}(x,y,\lambda) = f(x,y) + \lambda \cdot g(x,y)$
那么,求原函数极值的问题就转化为求该函数极值的问题。
类似地,这种求极值的方法也可以推广到多维函数$f(x_{1},\ldots,x_{n})$
三、举例
给定椭球:$ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} = 1$,求这椭球的内接最大长方体的体积。
这个问题实际上就是条件极值问题,即在条件$ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} = 1$下,求$f(x,y,z) = 8xyz$的最大值。这个问题当然可以用消元法解决,但我们在这里用的是拉格朗日乘数法。
首先定义拉格朗日函数$\mathcal{L}(x,y,z,\lambda) = 8xyz + \lambda \cdot (\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} - 1)$
之后解变量的偏导方程,对$\mathcal{L}(x,y,z,\lambda)$求偏导得:
$\dfrac {\partial{\mathcal{L}(x,y,z,\lambda)}} {\partial{x}} = 8yz + \dfrac {2 \lambda x}{a^2} = 0$
$\dfrac {\partial{\mathcal{L}(x,y,z,\lambda)}} {\partial{y}} = 8xz + \dfrac {2 \lambda y}{b^2} = 0$
$\dfrac {\partial{\mathcal{L}(x,y,z,\lambda)}} {\partial{z}} = 8xy + \dfrac {2 \lambda z}{c^2} = 0$
$\dfrac {\partial{\mathcal{L}(x,y,z,\lambda)}} {\partial{\lambda}} = \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} - 1 = 0$
联立前面三个方程得到$bx = ay$和$az = cx$,带入第四个方程解得:
$x = \dfrac{\sqrt{3}}{3}a$ $y = \dfrac{\sqrt{3}}{3}b$ $z = \dfrac{\sqrt{3}}{3}c$
带入解得内接长方体的最大体积为:$V_{max} = f(\dfrac{\sqrt{3}}{3}a,\dfrac{\sqrt{3}}{3}b,\dfrac{\sqrt{3}}{3}c) = \dfrac{8\sqrt{3}}{9}abc$
四、其他
维基百科上的这幅图画的很直观,特转自于此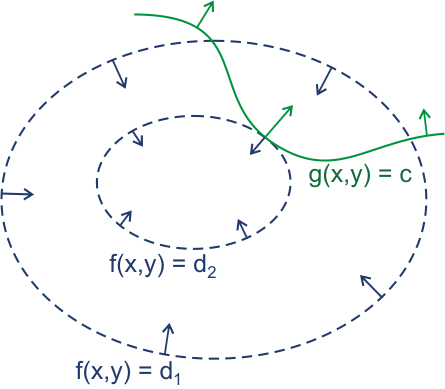
另外,拉格朗日乘数法只能求极值,不能精确到极小值或极大值(像求导求极值一样),所以要代入试验。