LeetCode DAY 3 (5)

11月 16 2019 LeetCode系列 21 分钟读完 (约 3155 字)

这些题都好难啊…越来越觉得自己是个铁fw了…呜呜呜

5. 最长回文子串（中等）

题目描述

给定一个字符串s，找到s中最长的回文子串。你可以假设s的最大长度为1000。

示例1:

1
2
3

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例2:

1 2	输入: "cbbd" 输出: "bb"

代码

解法1：暴力解法

作为一个铁fw第一个想到的办法肯定是暴力解决了，lz遍历你所有的子串还不能找出答案？具体做法就是两个for循环遍历所有子串，然后在最内循环里进行判断该子串是不是回文串。
因此我们需要定义一个判断是否为回文串的函数，该函数也很暴力，就直接遍历该子串看对应位置的字符是否相同。因此该算法的时间复杂度为$O(n^{3})$

#暴力解法，时间复杂度O(n^3) 空间复杂度O(1)
class Solution(object):
    def longestPalindrome(self, s):
        max = 0
        s_tmp = ''
        for i in range(0, len(s)):
            for j in range(i+1, len(s)+1):
                if self.isPalindrome(s[i:j]) and (j-i) > max :
                    s_tmp = s[i:j]
                    max = j-i
        return s_tmp
    #判断是否为回文串
    def isPalindrome(self, s):
        for i in range(0, len(s)/2):
            if(s[i] != s[len(s)-i-1]):
                return False
        return True

解法2：最长公共子串

还有一种办法就是求最长公共子串，具体做法就是将字符串反转，找出反转前后的公共子串，就是回文串（除一种情况外），比如'abad'，反转之后为'daba'，最长公共子串就是'aba'。
但是有一种情况除外，比如'abcdefgdcba'，反转之后为'abcdgfeabcd'，可以看到反转前后的最长公共子串为'abcd'，但它明显不是回文串，这种情况的特征是反转前后字符下标并不一致，因此求出反转前后的最长公共子串后我们需要判断下标是否对应。
但现在还有最后两个问题，怎么求最大公共子串以及下标是否对应如何判断。
看了大佬们的解析的我恍然大悟……奈何自己太菜…

求最长公共子串：
我们可以定义一个二维数组，可以想象成一个表格，横向代表原字符串序列，纵向代表反转后字符串序列，假设横向坐标用i表示，纵向坐标用j表示。数组用a表示。
当s[i] == s_r[j]时，就表示它是公共的一个字符，而此时对应的数组元素a[i][j] == a[i-1][j-1] + 1，因为a[i-1][j-1]的位置就是前一个连续的公共字符，因此a[i][j]的值就代表最长公共子串的长度，而此时的i代表该子串的结束位置，有了结束位置我们也就知道了开始位置，因此就可以取出该子串。
对于上面的计算公式a[i][j] == a[i-1][j-1] + 1，为了保证所有值有意义，我们需要分情况讨论，即当i == 0 or j == 0时进行赋值。该数组可参考下图所示：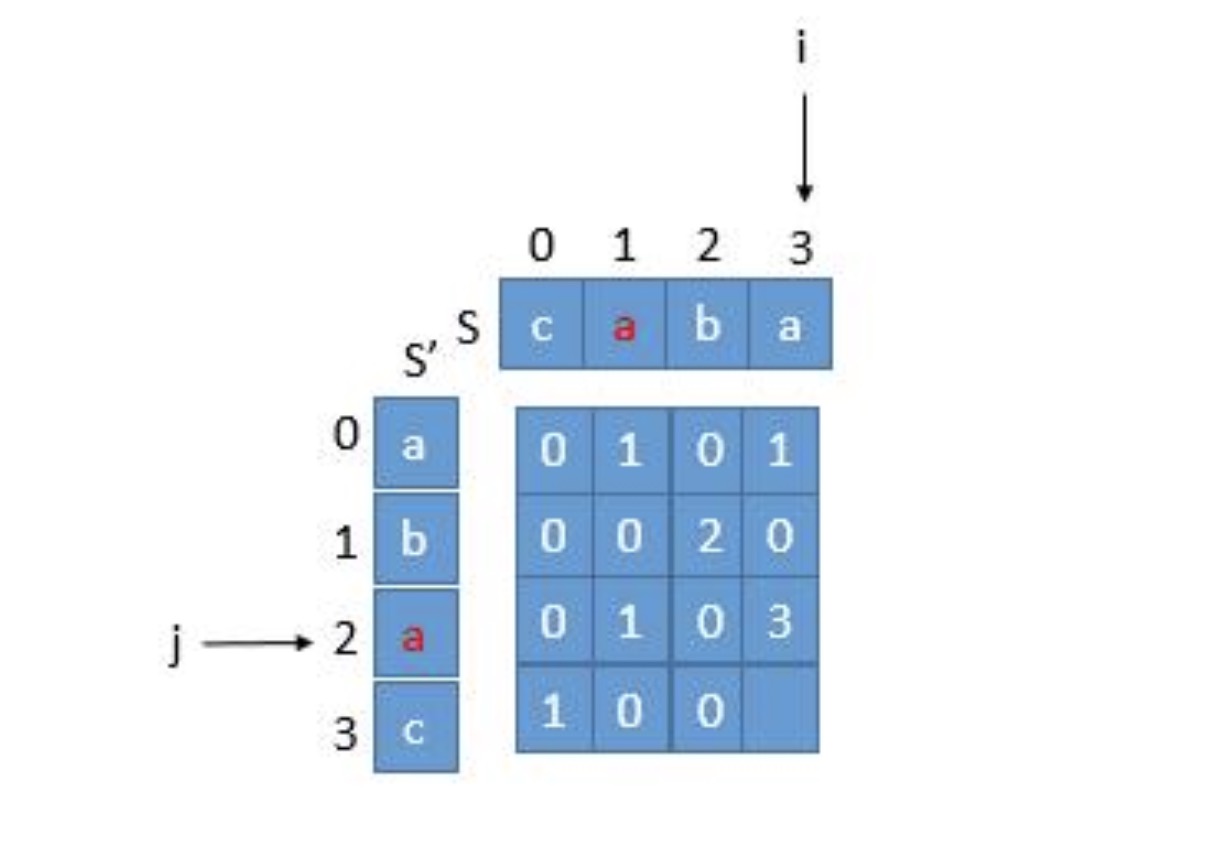
判断下标是否对应：
我们没有必要将公共子串的下标全部进行判断是否对应，我们只需要判断最后一个字符的下标。比如上图所示，我们将i和j对应公共子串的最后一个字符，现在s_re[j]的位置对应着a，那反转之前这个a的下标为before = len(s)-j-1，之后我们还需要加上公共子串的长度才是末尾字符的下标，因此判断before + a[i][j] - 1 == i，如果相等则为公共子串。

#时间复杂度O(n^2) 空间复杂度O(n^2)
class Solution(object):
    def longestPalindrome(self, s):
        s_reverse = s[::-1]
        max_len = 0 #最大公共子串长度
        max_end = 0 #最大公共子串结束位置
        index = {} #构建二维数组 python中只好先定义一个字典
        for i in range(0,len(s)):
            index[i] = {} #通过循环构建二维数组
            for j in range(0, len(s)):
                index[i][j] = 0 #初始化二维数组
                if s[i] == s_reverse[j]: 
                    if i==0 or j==0:
                        index[i][j] = 1
                    else:
                        index[i][j] = index[i-1][j-1] + 1
                if index[i][j] > max_len: 
                    before_num = len(s) - 1 - j
                    #判断是否真的是回文串
                    if before_num + index[i][j] - 1 == i:
                        max_len = index[i][j]
                        max_end = i
        return s[max_end-max_len+1:max_end+1]

但即使这个复杂度的代码提交还是时间超出限制我哭了，更低复杂度的代码等明天看懂再更……

解法3：暴力破解优化

在解法一中，我们对每一个子串都进行了判断是不是回文串，但每一次判断都会有$O(n)$的时间复杂度，如果我们能优化掉判断带来的时间复杂度，就可以将总的时间复杂度降为$O(n^{3})$，根据回文串的特点，在$P(i,j)$是回文串的基础上，如果s[i-1] == s[j+1]，那么$P(i-1,j+1)$也是回文串，因此我们将暴力解法中的判断函数改为这种判断方式。但有两种情况需要特殊对待，当子串的个数是1或者2时，此时的i-1和j+1将会将i和j的顺序颠倒产生错误，因此这两种情况需要额外判断。此外，我们需要定义一个数组，用来存储$P(i,j)$是否为回文串的结果。

#时间复杂度O(n^2) 空间复杂度O(n^2)
class Solution(object):
    def longestPalindrome(self, s):
        arra = [[0 for i in range(len(s))] for i in range(len(s))]
        max_len = 0
        max_str = ''
        for length in range(1, len(s)+1):
            for start in range(0, len(s)):
                end = start + length - 1
                if(end>=len(s)):
                    break
                if (length==1 or length==2 or arra[start+1][end-1]==1) and s[start] == s[end]:
                    arra[start][end] = 1
                    if length > max_len:
                        max_str = s[start:end+1]
                else:
                    arra[start][end] = 0
        return max_str

解法4：扩展中心

我们在解法3中提到，假设一个子串$P(i,j)$为回文串，如果s[i-1] == s[j+1]，那$P(i-1,j+1)$也是回文串，因此我们可以在已是回文串的子串的基础上进行中心扩展，那最初的中心怎么找呢？我们可以发现，最初的子串只有长度为1和长度为2两种情况，而长度为1的子串共有len(s)种，长度为2的子串共有len(s)-1种，因此我们应该循环2*len(s)-1次，在循环中判断此时中心是单个字符还是两个字符，之后进行中心扩展。

#时间复杂度O(n^2) 空间复杂度O(1)
class Solution(object):
    def longestPalindrome(self, s):
        max_len = 0
        max_str = ''
        for i in range(2*len(s) - 1):
            if i % 2 == 1:
                start = (i-1) // 2
                end = start + 1
                if(s[start] == s[end]):
                    while start > 0 and end < len(s)-1 and s[start-1] == s[end+1]:
                        start -= 1
                        end += 1
            else:
                start = end = i // 2
                while start > 0 and end < len(s)-1 and s[start-1] == s[end+1]:
                    start -= 1
                    end +=1
            if (end-start+1) > max_len and s[start]==s[end]:
                max_len = end-start+1
                max_str = s[start:end+1] 
        return max_str

解法5：Manacher’s Algorithm 马拉车算法

解法5 转自 LeetCode 用户 windliang 的题解。

马拉车算法Manacher‘s Algorithm是用来查找一个字符串的最长回文子串的线性方法，由一个叫 Manacher 的人在 1975 年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性。

预处理

首先我们解决下奇数和偶数的问题，在每个字符间插入”#”，并且为了使得扩展的过程中，到边界后自动结束，在两端分别插入”^”和 “$”，两个不可能在字符串中出现的字符，这样中心扩展的时候，判断两端字符是否相等的时候，如果到了边界就一定会不相等，从而出了循环。经过处理，字符串的长度永远都是奇数了。

我们用一个数组P保存从中心扩展的最大个数，而它刚好也是去掉”#”的原字符串的总长度。例如下图中下标是6的地方，可以看到P[6]等于5，所以它是从左边扩展5个字符，相应的右边也是扩展5个字符，也就是#c#b#c#b#c#。而去掉#恢复到原来的字符串，变成cbcbc，它的长度刚好也就是5。

求原字符串下标

用P的下标减去P[i]，再模2，就是原字符串的开头字符下标了。
例如我们找到P[i]的最大值为5，也就是回文串的最大长度是5，对应的下标是6，所以原字符串的开头下标是(6 - 5)/ 2 = 0。所以我们只需要返回原字符串的s[0:5]就可以了。

求每个`P[i]`

接下来是算法的关键了，它充分了利用了回文串的对称性。

我们用C表示回文串的中心，用R表示回文串的右边半径。所以R = C + P[i]。C和R所对应的回文串是当前循环中R最靠右的回文串。

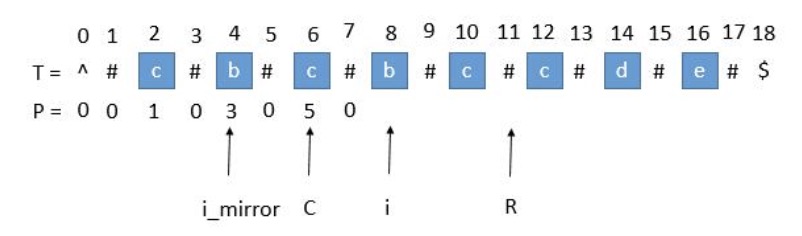
我们考虑求P[i]的时候，用i_mirror表示当前需要求的第i个字符关于C对应的下标。
现在要求P[i]，如果是用中心扩展法，那就向两边扩展比对就行了。但是我们其实可以利用回文串C的对称性。i关于C的对称点是i_mirror，P[i_mirror] = 3，所以P[i] 也等于3。
但是有三种情况将会造成直接赋值为P[i_mirror]是不正确的，下边一一讨论。
1. 超出了R

当我们要求P[i]的时候，P[mirror] = 7，而此时P[i]并不等于7，为什么呢，因为我们从i开始往后数7个，等于22，已经超过了最右的R，此时不能利用对称性了，但我们一定可以扩展到R的，所以P[i]至少等于R - i = 20 - 15 = 5，会不会更大呢，我们只需要比较T[R+1]和T[R+1]关于 i 的对称点就行了，就像中心扩展法一样一个个扩展。
2. P[i_mirror]遇到了原字符串的左边界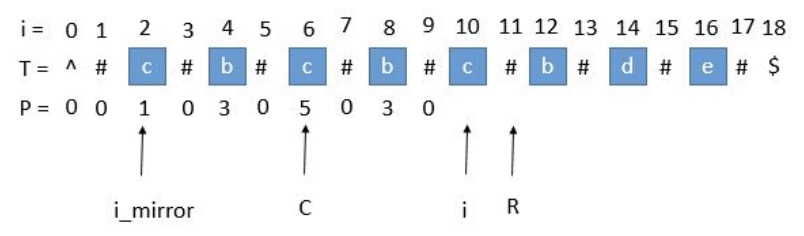

此时P[i_mirror] = 1，但是P[i]赋值成1是不正确的，出现这种情况的原因是P[i_mirror]在扩展的时候首先是'#' == '#'，之后遇到了 '^' 和另一个字符比较，也就是到了边界，才终止循环的。而P[i]并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。
2. i == R
此时我们先把P[i]赋值为0，然后通过中心扩展法一步一步扩展就行了。

考虑`C`和`R`的更新

就这样一步一步的求出每个P[i]，当求出的P[i]的右边界大于当前的R时，我们就需要更新C和R为当前的回文串了。因为我们必须保证i在R里面，所以一旦有更右边的R就要更新R。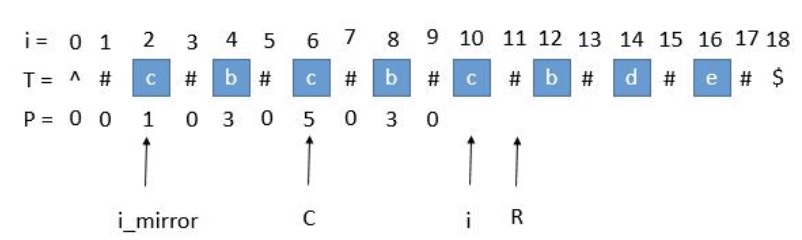

此时的P[i]求出来将会是3，P[i]对应的右边界将是10 + 3 = 13，所以大于当前的R，我们需要把C更新成i的值，也就是10，R更新成13。继续下边的循环。

class Solution(object):
    #字符串预处理
    def preprocess(self, s):
        if len(s) == 0:
            return '$'
        else:
            ret = '^'
            for i in range(len(s)):
                ret += '#'+s[i]
            return ret + '#$'

    def longestPalindrome(self, s):
        #预处理
        t = self.preprocess(s)
        P, C, R = [0 for i in range(len(t))], 0, 0
        for i in range(1,len(t)-1):
            i_mirror = 2*C-i
            if(R>i): #保证i在R内
                P[i] = min(R-i, P[i_mirror])
            else: #i<=R的时候
                P[i] = 0
            #上面说的三种情况
            #因为其余情况下P[i]已确定，因此不会进入循环
            while t[i+1+P[i]] == t[i-1-P[i]]:
                P[i]+=1
            #更新C和R
            if i + P[i] > R:
                C = i
                R = i + P[i]
        len_max = 0
        centerIndex = 0
        for i in range(1, len(t)-1):
            if P[i] > len_max:
                len_max = P[i]
                centerIndex = i
        #根据公式计算start
        start = (centerIndex - len_max)/2
        return s[start:start+len_max]